Platons Höhlengleichnis als Leitmotiv der Mathematik

Jedem Mathematiker ist geläufig, dass im Aufbau des mathematischen Gedankengebäudes immer wieder unvollkommene Strukturen durch vollkommenere ersetzt werden, die entweder als bereits vorhanden erkannt werden oder (häufiger) gänzlich neu erfunden werden. Hierfür soll eine Reihe prägnanter Beispiele gegeben werden, die, so hoffe ich, auch für Nichtmathematiker zugänglich und informativ sind. Der mathematische Schöpfungsprozess, der dabei stattfindet, wird mit einem Grundgedanken aus Platons Philosophie verglichen.

Platons Politea und das Höhlengleichnis

Platons großes Werk Politeia (der Staat) entstand um das Jahr -400. Es hat die Form eines fiktiven Gesprächs zwischen Platons Lehrer Sokrates und Platons Brüdern Glaukon und Adeimantos.  Im siebenten Buch beginnt Platon, die Methodik der Erziehung künftiger Philosophen-Regenten, also der staatslenkenden Elite,  zu diskutieren. Hier dient das Höhlengleichnis als Ausgangspunkt und Grundlage; es soll die menschliche Natur in Bezug auf Unbildung und Bildung beleuchten.

Das Höhlengleichnis schildert die Situation von Menschen, die ihr Leben in einer Höhle verbringen, und die so gefesselt sind, dass sie nur die dem Eingang gegenüberliegende Rückwand der Höhle sehen können. Vor dem Höhleneingang werden Gegenstände vorbeigetragen, die auf dieser Rückwand undeutliche Schatten werfen. Die Höhlenbewohner entwickeln Theorien, die Vorhersagen über das Verhalten der Schatten erlauben sollen. Wer dies am besten kann, hat unter ihnen das höchste Ansehen.

Es wird nun durchgespielt, was geschieht, wenn ein Höhlenbewohner die Kraft aufbringt, sich zu befreien und ans Tageslicht zu gelangen. Er wird dann geblendet sein und erst allmählich die schattenwerfenden Gegenstände erkennen. Erst viel später erkennt er auch die Verursacherin der Schatten, die Sonne. Sie steht hier für die Idee des Guten, das ultimative Ziel des Erkenntnisstrebens und so etwas wie der heilige Gral in Platons Philosophie. Kehrt nun dieser Mensch in die Höhle zurück, so wird er ein zweites Mal blind, diesmal weil seine Augen an das Licht der Sonne gewöhnt sind und in der Finsternis nichts mehr wahrnehmen. Die Erkenntnisse, die er von seiner Reise mitbringt, werden von den Zurückgebliebenen abgelehnt, er selbst wird angefeindet und gar ermordet.

Jede Einzelheit dieses Gleichnisses kennt jeder Mensch, der für den Erkenntnisgewinn lebt, aus eigener Erfahrung.  Die zweimalige eigene Blindheit und die Ablehnung mühsam gewonnener Erkenntnis gehört unbedingt dazu, und als Mathematiker hat man besonders viel Gelegenheit, diese Erfahrung zu machen.

Hier soll es besonders um den Weg zu den schattenwerfenden Gegenständen gehen. Zu betonen ist, dass wir hier Platons Gedankenwelt verlassen. Für ihn gehört die Mathematik zwar unbedingt zur Erziehung der Philosophen-Regenten, aber nur als erste Stufe, mit einem propädeutischen Anspruch.  Platon stellt vollkommen richtig fest, dass die Mathematik immer von Annahmen ausgeht. Das bedeutet für ihn, dass sie keine Erkenntnis über die Wirklichkeit gewinnen kann.  Auch hier muss man zustimmen; anders sieht es erst aus, wenn die Mathematik sich mit Naturwissenschaften verbindet.

Rekonstruktion existierender Objekte aus ihren Schatten

Hier geht es um Beispiele, bei denen ein Gegenstand untersucht werden soll, der direkt  nicht zugänglich ist und von dem nur ein Schatten zu sehen ist. In allen anderen Abschnitten wird es dagegen darum gehen, den gewünschten in irgendeinem Sinne vollkommenen Gegenstand in freier Schöpfung zu erschaffen.

Das erste Beispiel handelt unmittelbar von der Höhlensituation. In der Darstellenden Geometrie werden von räumlichen Gebilden, z.B. einem Würfel, Schatten gezeichnet wie sie bei Beleuchtung mit parallelem Licht (etwa von der Sonne) auf eine ebene Fläche geworfen werden. Es geht nun um die Frage, ob jede Zeichnung dieser Art, die auf den ersten Blick so aussieht, als sei es der Schatten eines Würfels, tatsächlich als Bild eines wirklichen Würfels erzeugt werden kann.  Die positive Antwort auf diese Frage wurde von Karl Wilhelm Pohlke 1853 gefunden und von Hermann Amandus Schwarz vollständig bewiesen, was gar nicht einfach ist. Trotzdem beeindruckt dieses Ergebnis wenig; das liegt daran, dass unser Gehirn durch lebenslanges Training schon weiß, dass es richtig ist.

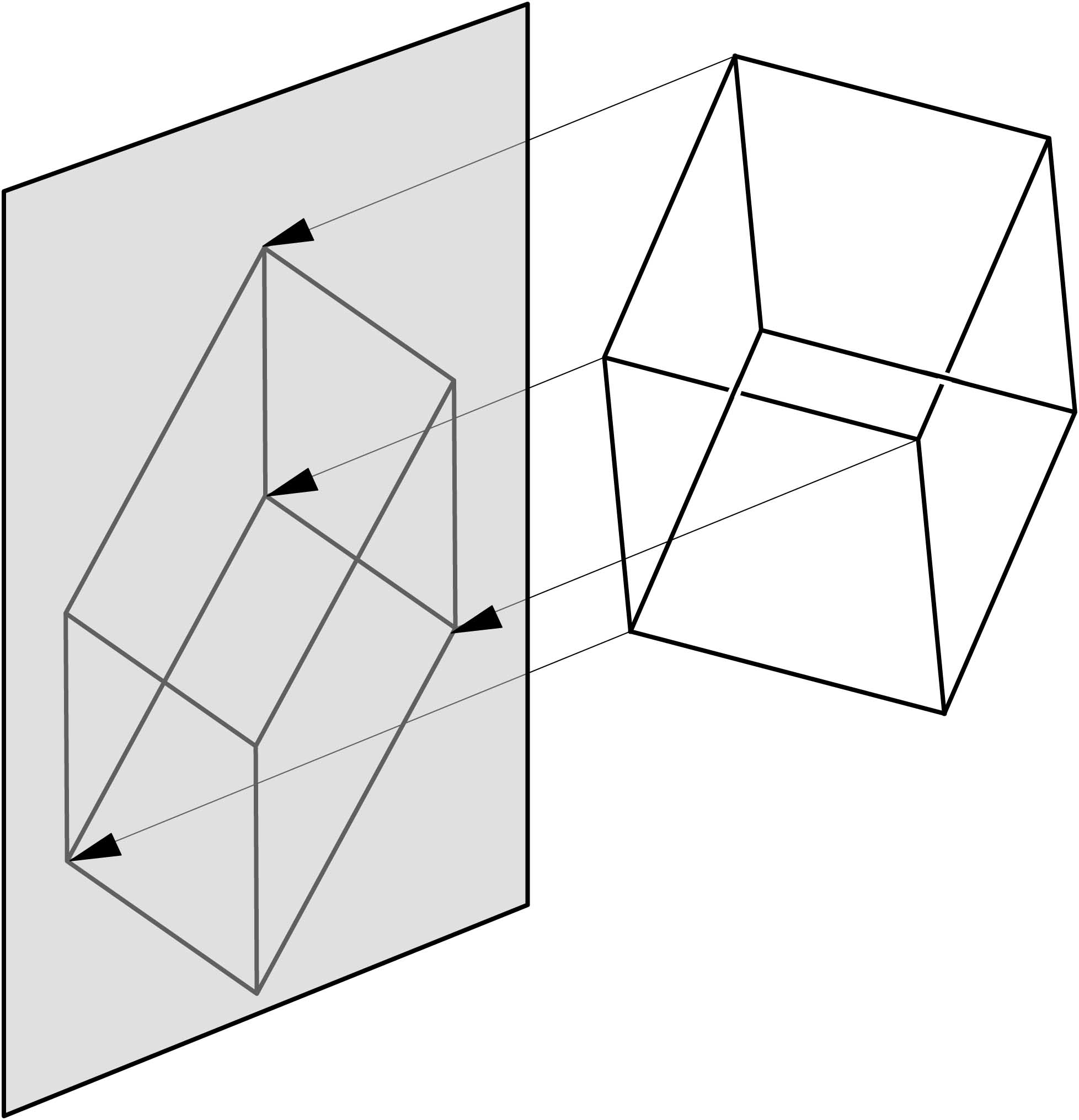
In der nächsthöheren Dimension ist unser Gehirn nicht vorbereitet, aber das Phänomen tritt ebenfalls auf. Ob der Satz von Pohlke auch hier gilt, ist mir nicht bekannt. Jedenfalls kann jeder, der nach Paris reist, den Schatten eines vierdimensionalen Würfels im dreidimensionalen Raum bewundern, nämlich in Gestalt des Gebäudes La Grande Arche, hier im Foto zu sehen. Der dreidimensionale Würfel hat in jeder Achsenrichtung zwei Quadrate als Seiten. Bei drei Achsen macht das sechs Quadrate. Im vierdimensionalen Raum gibt es vier Achsen, daher hat der vierdimensionale Würfel zwei mal vier Seiten, also acht dreidimensionale Seitenwürfel. Diese sind in ganz bestimmter Weise miteinander verbunden, das wird durch das Gebäude dargestellt. Von den acht Würfeln sind nur vier materiell ausgeführt, man sieht sie (zu Pyramidenstümpfen deformiert) oben, unten, rechts und links. Die anderen vier Würfel muss man sich hinzudenken: einer vorn, einer hinten, einer, der das ganze Gebäude umschließt, und einer, der in der Mitte zwischen den nach innen gewandten Flächen sitzt.

Ein praktisch hochrelevantes Beispiel ist die Computertomographie. Ein einzelnes Röntgenbild des menschlichen Körpers ist eine Verteilung von Grauwerten auf einer Bildebene. Jeder einzelne Bildpunkt zeigt durch seinen Grauwert an, wie stark die Röntgenstrahlen auf dem Weg durch den Körper  zu diesem Punkt vom Körpergewebe geschwächt wurden. Mathematisch ist dieser Wert als Integral über den Weg des Röntgenstrahls zu deuten. Wie bei einem Schatten auf der Höhlenwand lässt sich hieraus nicht ermitteln, wie die verschiedenen schwächenden Einflüsse auf den Röntgenstrahl räumlich im Körper verteilt sind. Das ändert sich, wenn man viele Röntgenbilder aus verschiedenen Blickrichtungen hat. Es ist allgemein bekannt, dass daraus ein detailliertes räumliches Bild der inneren Organe gewonnen werden kann. Der Name Computertomographie verweist auf den hohen Rechenaufwand, der erst durch den Einsatz von Computern beherrschbar wurde. Die Grundlage, auf der dies geschieht, ist jedoch eine mathematische Arbeit von Johann Radon aus dem Jahre 1917, als Röntgenstrahlen zwar schon bekannt waren, aber Computer noch nicht entwickelt waren. Die Arbeit mit dem Titel Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten erschien in den Berichten über die Verhandlungen der Königlich-Sächsischen Akademie der Wissenschaften zu Leipzig. Sie klärt die Bedingungen, unter denen diese Rekonstruktionsaufgabe lösbar und die Lösung eindeutig ist, und sie gibt eine Methode zu deren Berechnung an.

Die Naturwissenschaften bieten eine Fülle von Beispielen für diesen Typ von Problemlösungen, also für die Rekonstruktion eines Objekts oder Vorgangs aus irgendwelchen davon verursachten Spuren. Hierunter fällt etwa die detaillierte Rekonstruktion eines  Zerfalls von Elementarteilchen nach einer Kollision,  ausgehend von den Flugbahnen der Zerfallsprodukte, ihren Winkeln und Krümmungen.

Selbstdurchdringung: Die Kleinsche Flasche

Platon hält den Mathematikern gern vor, sie würden Bilder zeichnen und über sie reden, aber sie meinten dabei etwas ganz anderes als das Dargestellte. In der Tat, die Bilder, die Mathematiker zeichnen, sind nichts als Schatten der eigentlich gedachten Objekte, und sie sollen nur dazu dienen, unserem Gehirn etwas anzubieten, womit es dank seines Trainings seit Kleinkindzeit etwas anfangen kann. Ein schönes Beispiel hierfür sind die Bilder, man die üblicherweise von der sogenannten Kleinschen Flasche, einer bestimmten in sich geschlossenen Fläche ohne Rand, zeichnet. Statt durch eine Zeichnung stelle ich sie hier zunächst durch ein Foto einer Glasbläserarbeit vor (Abb.3).

Auch diese Glasbläserarbeit ist nicht wirklich die Kleinsche Flasche, sondern ein Schatten von ihr im dreidimensionalen Raum. Wirklich realisieren lässt sie sich nur in vier Dimensionen.  Beschreiben wir sie kurz: der Flaschenhals dringt an einer Stelle durch die Wand der Flasche ins Innere ein und geht unten nahtlos in den Boden und dann in die Wand der Flasche über. Der Defekt dieser Darstellung liegt in der Selbstdurchdringung. An dieser Stelle muss man jeden Punkt des Modells doppelt zählen, einmal als Punkt der Wand und einmal als Punkt des Halses. Macht man eine Kartendarstellung einer Eisenbahnunterführung, so hat man dasselbe Problem, nur eine Dimension niedriger. In der zweidimensionalen Kartendarstellung hat die Straße mit der Bahnlinie einen gemeinsamen Punkt. In Wirklichkeit ist an dieser Stelle das Gleis in Richtung der dritten Dimension angehoben und es gibt keine Kreuzung. Ebenso muss man sich den Hals der Kleinschen Flasche an der Durchdringungsstelle in Richtung der vierten Dimension angehoben denken.

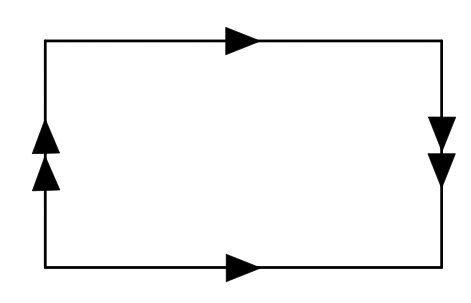
In Wirklichkeit arbeiten Mathematiker, wenn es um die Kleinsche Flasche (und viele andere Gebilde) geht mit einer noch viel stenographischeren Bildsprache (Abb.4). Abb.4 ist zu lesen als Darstellung der Fläche eines Quadrats, das an seinen Rändern mit sich selbst verklebt ist, so, wie es den beiden Pfeilpaaren entspricht. Das heißt, die beiden Kanten mit einfachen Pfeilen werden gleichlaufend aneinandergeklebt, um eine Röhre zu bilden, und dann werden die Kanten mit Doppelpfeilen  gemäß Pfeilrichtung, also verdreht, zusammengeklebt. Das ergibt dann den Übergang vom Hals der Flasche in den Boden und die Wand. Der Vorgang ist im dreidimensionalen Raum nicht durchführbar, aber das hindert uns nicht, diese Skizze wie eine Landkarte der Fläche zu lesen und darin zu navigieren. Auch dies bestätigt wieder die Richtigkeit von Platons Wahrnehmung.

Euklid

Platons Kritik an der Mathematik geht noch weiter. Es sagt, die Mathematiker kennen nicht die Gegenstände, von denen sie reden. Sie gehen immer nur von Annahmen aus. Auch hier hat er sehr scharfsinnig getroffen. Am besten lässt sich das an Euklids axiomatischem Aufbau der Geometrie feststellen. Euklid beginnt zwar mit Definitionen für Punkte und Geraden. Aber die Definition von Punkten: Σημεῖόν ἐστιν, οὗ μέρος οὐθέν (Punkt ist, was keinen Teil hat)  wird im weiteren niemals benutzt, sie steht komplett außerhalb der Theorie. Der Begriff Punkt ist eine Abstraktion für Dinge unserer Wirklichkeit, es ist die Idee dieser Dinge. Die seltsame Definition hat höchstens den Sinn, diesen abstrakten Begriff mit seinem Schatten in unserer Wirklichkeit zu verknüpfen. Die wesentlichen Axiome bei Euklid behandeln ausschließlich die Beziehungen von Punkten und Geraden untereinander, also zum Beispiel, dass zwei verschiedene Geraden entweder keinen oder genau einen Punkt gemeinsam haben.

Von der affinen zur projektiven Geometrie

Die Geraden der Ebene haben, wie eben festgestellt, die Eigenschaft, dass zwei von ihnen sich schneiden können oder auch nicht. Der letztere Ausnahmefall (Parallelität) ist eine Unvollkommenheit der ebenen Geometrie, die für viel Aufwand bei der Beschreibung von Sachverhalten und beim Beweis von allgemeinen Aussagen sorgt. Das Ziel ist, diese "affine" ebene Geometrie als Schattenbild einer vollkommeneren Geometrie, der "projektiven Geometrie" zu deuten.  Längen- und Winkelbegriff bleiben dabei ausgeklammert.

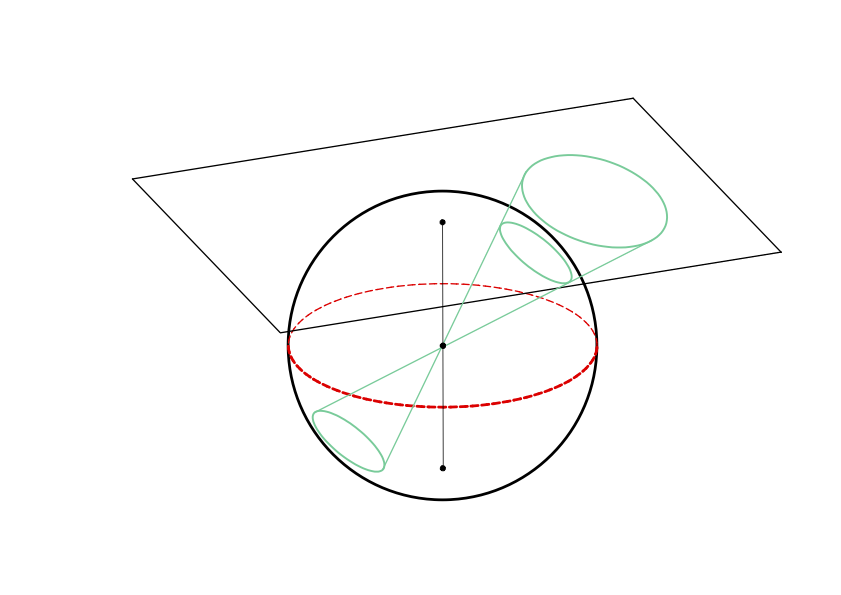
Wir wollen die projektive Geometrie aus den Großkreisen auf einer Sphäre (Kugeloberfläche) gewinnen (Abb.5). Dabei ist ein Großkreis ein Kreis auf der Sphäre, der denselben Mittelpunkt hat wie die Sphäre. Einer davon sei als Äquator ausgezeichnet (rot, gestrichelt), und wir legen die affine Ebene so, dass sie die Sphäre im Nordpol berührt; der Äquator liegt dann in einer zu ihr parallelen Ebene.

Stellen wir nun eine punktförmige Lichtquelle in den Kugelmittelpunkt, so werfen alle Großkreise mit Ausnahme des Äquators einen geradlinigen Schatten in der affinen Ebene. Die nördliche Hemisphäre mit den in ihr liegenden Teilen der Großkreise erweist sich so als exakte Kopie der affinen Ebene.

Nun kommt der wesentliche Schritt. Wir ergänzen die Hemisphäre zur kompletten Sphäre einschließlich  Äquator und nehmen die kompletten Großkreise einschließlich des Äquators als neue Geraden. Zwei verschiedene Großkreise schneiden sich ausnahmslos in einem Paar diametral gegenüberliegender Punkte. Diese Paare nehmen wir als unsere neuen Punkte, und damit haben wir die projektive Ebene; sie besteht aus den neuen Punkten und den neuen Geraden. Eine Entsprechung in der affinen Ebene haben nur diejenigen neuen Punkte, die nicht auf dem Äquator liegen, und die neuen Geraden, die vom Äquator verschieden sind. Zwei von den letzteren entsprechen einem parallelen Geradenpaar alter Art, wenn ihr Schnittpunktepaar auf dem Äquator liegt.

Da es keine Parallelen mehr gibt, zwei verschiedene Geraden schneiden sich jetzt immer in einem Punkt, ist die projektive Geometrie wesentlich einfacher als die affine. Viel wichtiger ist jedoch, dass sie auch wesentlich symmetrischer ist. Man sieht das schon daran, dass die neu hinzuerfundene "uneigentliche" Gerade (der Äquator) mit den anderen Geraden völlig gleichberechtigt ist: Man kann ja die Sphäre beliebig drehen, ohne dass sich an der Geometrie der Großkreise etwas ändert.

Noch dramatischer zeigt sich die Vollkommenheit der projektiven Geometrie, wenn man Kegelschnitte betrachtet. In der Schule habe ich drei Arten von Kegelschnitten unterscheiden gelernt: Ellipsen, Parabeln und Hyperbeln. Zu jeder Sorte musste eine eigenständige Theorie entwickelt werden. Die drei Theorien glichen einander stark, aber waren im Detail sehr unterschiedlich. (In meiner Schulzeit gab es natürlich längst die projektive Geometrie, aber sie wurde nicht behandelt.)

Projektiv betrachtet gibt es dagegen nur eine einzige Art von Kegelschnitten. Ein Kegelschnitt entsteht in der affinen Ebene, wenn man einen Kegelmantel nimmt, dessen Spitze der Kugelmittelpunkt ist, und die Linie anschaut, wo die Kegelfläche die affine Ebene durchdringt (die affine Ebene ist dabei nach wie vor die Ebene, die die Sphäre im Nordpol berührt). Wie im Bild dargestellt, entsteht eine Ellipse, falls der Kegel den Äquator nicht trifft. Trifft er den Äquator in einem oder in zwei Paaren von Diametralpunkten, so entsteht eine Parabel bzw. eine Hyperbel.  Man bekommt so eine einheitliche Theorie aller Kegelschnitte, und die Symmetrie dieser Geometrie ist so stark, dass alle Kegelschnitte durch Symmetrien ineinander überführt werden können.

Die Entwicklung des modernen Zahlbegriffs

Vom antiken Griechenland bis heute zieht sich eine lange Entwicklung. Sie besteht im wesentlichen in einer Serie von Neuschöpfungen, von denen jede einzelne im Sinne des Höhlengleichnisses gedeutet werden kann, weil sie das jeweils vorhandene Zahlenreich als Teil eines größeren und vollkommeneren erweist. Bei jedem der Schritte, die im folgenden vorgeführt werden, ist der Ausgangspunkt eine Einschränkung, ein Defizit, an dem das vorhandene Zahlsystem leidet, meist in Gestalt einer unlösbaren Gleichung. Jedesmal besteht die Abhilfe darin, neue "Jokerzahlen" zu erfinden, die genau die bis dahin unlösbaren Gleichungen lösen. Es ist natürlich nie selbstverständlich, dass das erlaubt ist. Man muss immer erklären, wie mit den neuen Zahlen zu rechnen ist und vor allem zeigen, dass durch die Erweiterung nicht Rechengesetze verloren gehen, auf die man angewiesen ist, wie zum Beispiel das Distributivgesetz a(b + c) = ab + ac. Hierauf wird im folgenden nicht näher eingegangen. Betont sei aber noch, dass es nicht möglich ist, einzelne Zahlen zu definieren (ebensowenig wie einzelne Punkte und Geraden), nur ganze Zahlsysteme mit ihren Rechengesetzen lassen sich sinnvoll einführen.

Ganz am Anfang stehen die natürlichen Zahlen, wie wir sie beim Zählen verwenden, also 1, 2, 3, 4, 5 und so weiter. Man kann sie addieren und multiplizieren und manche Gleichungen lösen, zum Beispiel die Gleichung  3 + x = 5 , aber nicht die Gleichung 5 + x = 5 . Die Jokerzahl, die dieses Defizit beseitigt, ist die Null, und es hat erstaunlich lange gedauert (bis zum 17. Jahrhundert), bis sich dieser Joker als gleichberechtigte Zahl (und nicht nur als Ziffer wie in der Zahl 10) durchgesetzt hat.

Ähnlich schwer fiel die Einführung der negativen Zahlen als Lösungen von Gleichungen wie 5 + x = 3, womit wir beim System der ganzen Zahlen angelangt sind. Die rationalen Zahlen oder Brüche als Lösungen von Gleichungen wie  5 · x = 3 waren hingegen im Prinzip bereits den Griechen vertraut, die allerdings nicht unsere Bruchschreibweise 3/5  verwendet haben, sondern das Zahlenverhältnis  3 : 5 betrachtet haben.  Eigentlich erstaunlich, denn die Einführung der Brüche wie der Zahlenverhältnisse erfordert, dass man sich über die Gleichheit von Brüchen oder von Verhältnissen Gedanken macht, also erklären muss, warum   3/5 dasselbe ist wie 6/10 . Das ist bei der Einführung der negativen Zahlen viel einfacher.

Die Philosophenschule der Pythagoreer im alten Griechenland  liebte die Verhältnisse ganzer Zahlen. Es wird behauptet, sie hätten am liebsten alle Beziehungen zwischen Dingen durch Zahlenverhältnisse erklärt. Leider mussten sie feststellen, dass dies nicht einmal im Reich der Geometrie möglich ist, wenn man nämlich Streckenlängen durch Zahlen beschreiben will. Ausgerechnet am Logo der Pythagoreer, dem Pentagramm (also dem regelmäßigen Fünfeck) lässt sich demonstrieren, dass die rationalen Zahlen hierfür nicht ausreichen.

Im Pentagramm bezeichnen wir die (Länge der) Seite mit a  und die Diagonale mit b. Stünden diese beiden Zahlen in einem ganzzahligen Verhältnis, so gäbe es ein gemeinsames Maß, also eine Strecke c, aus denen a  und b  beide durch ganzzahliges Vervielfachen entstehen. Wenn das der Fall wäre, könnte man c  durch ein von den Griechen erfundenes Verfahren bestimmen, die sogenannte Wechselwegnahme,  heutigen Mathematikern als Euklidischer Algorithmus bekannt. Man zieht von einer der Zahlen ein möglichst großes Vielfaches der anderen ab und ersetzt sie durch den Rest, der übrig bleibt. Dann macht man es umgekehrt, und wiederholt es so lange bis ein Rest Null auftritt. Dann hat man das gemeinsame Maß gefunden.

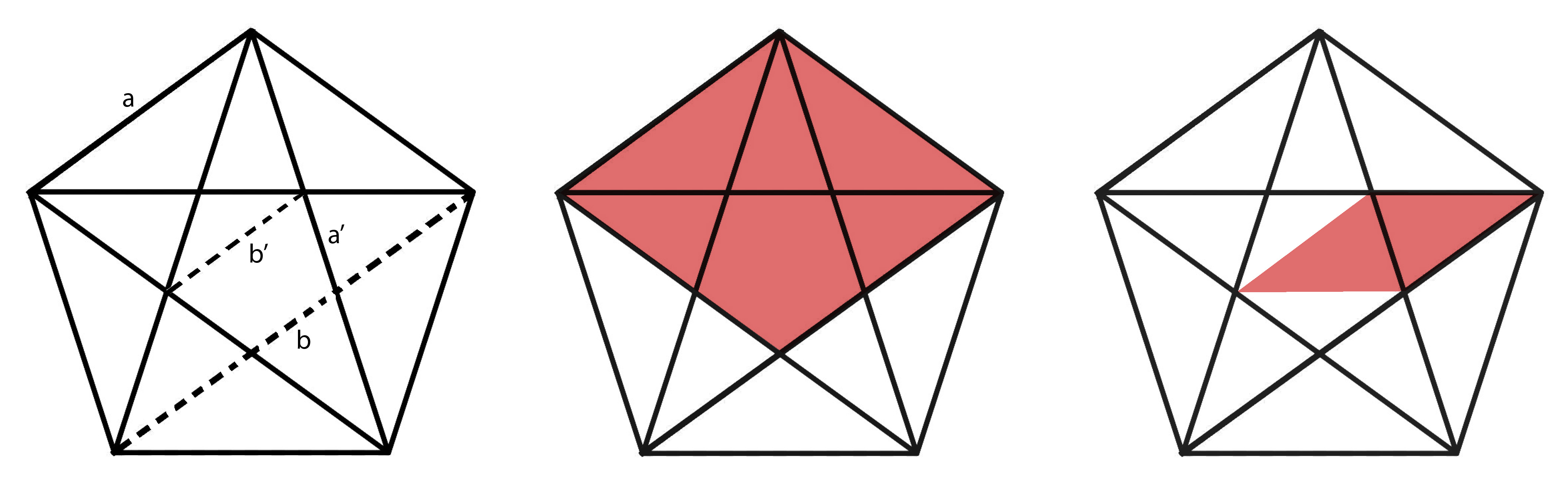
Beim Pentagramm und den Zahlen a  und b  ist es nun so, dass zwei Schritte der Wechselwegnahme auf die Seite a' und die Diagonale  b' des kleinen Fünfecks führen, das man in der Mitte des Pentagramms erkennt. Es gilt nämlich, wie man an zwei in der Figur versteckten Parallelogrammen erkennt, dass  b -a = b' ist und b - 2b'= a'. Auch bei allen Wiederholungen der Wechselwegnahme bleibt also nie der Rest Null. 

Der Wert des Verhältnisses  von Seite und Diagonale im regelmäßigen Fünfeck ist der goldene Schnitt

 b:a=(1/2+ 1/2 √5):1.

Dabei bedeutet  √5 eine Jokerzahl, die die in den rationalen Zahlen nachweislich unlösbare Gleichung x · x = 5 löst. Zahlen solcher Form sind ein erstes Beispiel  der algebraischen Zahlen, d.h. der Lösungen von Polynomgleichungen mit rationalen Koeffizienten, wie etwa der Gleichung x⁵  - 5x +1 = 0.

Allerdings entsteht jetzt ein neues Problem. Evariste Galois (1811-1832) hat nämlich gezeigt und kurz vor seinem Tod im Duell aufgeschrieben, dass zum Beispiel die Lösungen der letzten Gleichung sich nicht wie der goldene Schnitt durch Wurzelausdrücke hinschreiben lassen. Da es unendlich viele derartige Gleichungen gibt, kommt man mit dem Einführen einzelner Jokerzahlen nicht weit, man braucht einen Generalangriff, der die (reellen) algebraischen Zahlen und noch viel, viel mehr liefert.

Dies ist eine große Leistung des Braunschweiger Mathematikers Richard Dedekind. In seinem Werk Stetigkeit und irrationale Zahlen, Braunschweig, Vieweg, 1872, erschafft er ein Zahlen-Kontinuum, die reellen Zahlen,  durch die Einführung eines Super-Jokers, nämlich der heute nach ihm benannten Dedekindschen Schnitte. Damit realisiert er etwas, was auch den alten Griechen vage vorgeschwebt hat.

Ein Dedekindscher Schnitt ist nichts als eine Einteilung aller rationalen Zahlen in zwei Mengen A  und B, wobei jede Zahl aus A  kleiner ist als jede Zahl aus B. Dadurch wird eine Jokerzahl festgelegt, die in die eventuell vorhandene Lücke zwischen A  und B  hineinpasst. Dadurch erreicht man, dass alle derartigen Lücken geschlossen werden, es entsteht ein lückenloser Zahlbereich, in dem stetige Bewegungen möglich sind. Man erhält so einen großen Teil aller algebraischen Zahlen, die reellen algebraischen Zahlen: Die linke Seite der zuletzt aufgeschriebenen Polynomgleichung etwa nimmt positive und negative Werte an. Da die Zahl x  in einem Bereich ohne Lücken variiert, kann man zeigen, dass auch die Werte der linken Seite keine Lücken aufweisen, und somit kommt der Wert Null vor (dies ist ein sogenanntes Stetigkeitsargument).

Trotzdem sind die algebraischen Zahlen nur ein verschwindend kleiner Teil der reellen Zahlen, zu denen auch manche Prominente gehören wie etwa die Kreiszahl π oder die Eulerzahl  e.

Wir sind immer noch nicht am Ziel, denn die Polynomgleichung x · x = -1 hat noch keine Lösung. Um das zu beheben, reicht die Einführung einer einzigen Jokerzahl, der imaginären Einheit i = √-1.

Damit haben wir die komplexen Zahlen a + b√-1 oder a + bi  mit beliebigen reellen Zahlen a, b. In diesem wundervollen Zahlenbereich hat jetzt jede Polynomgleichung (auch mit komplexen Koeffizienten) mindestens eine Lösung. Einer von vielen Beweisen dieses Fundamentalsatzes der Algebra stammt von Gauß, ebenfalls einem großen Braunschweiger. Man benutzt am besten wieder Stetigkeitsargumente auf etwas höherer Stufe.

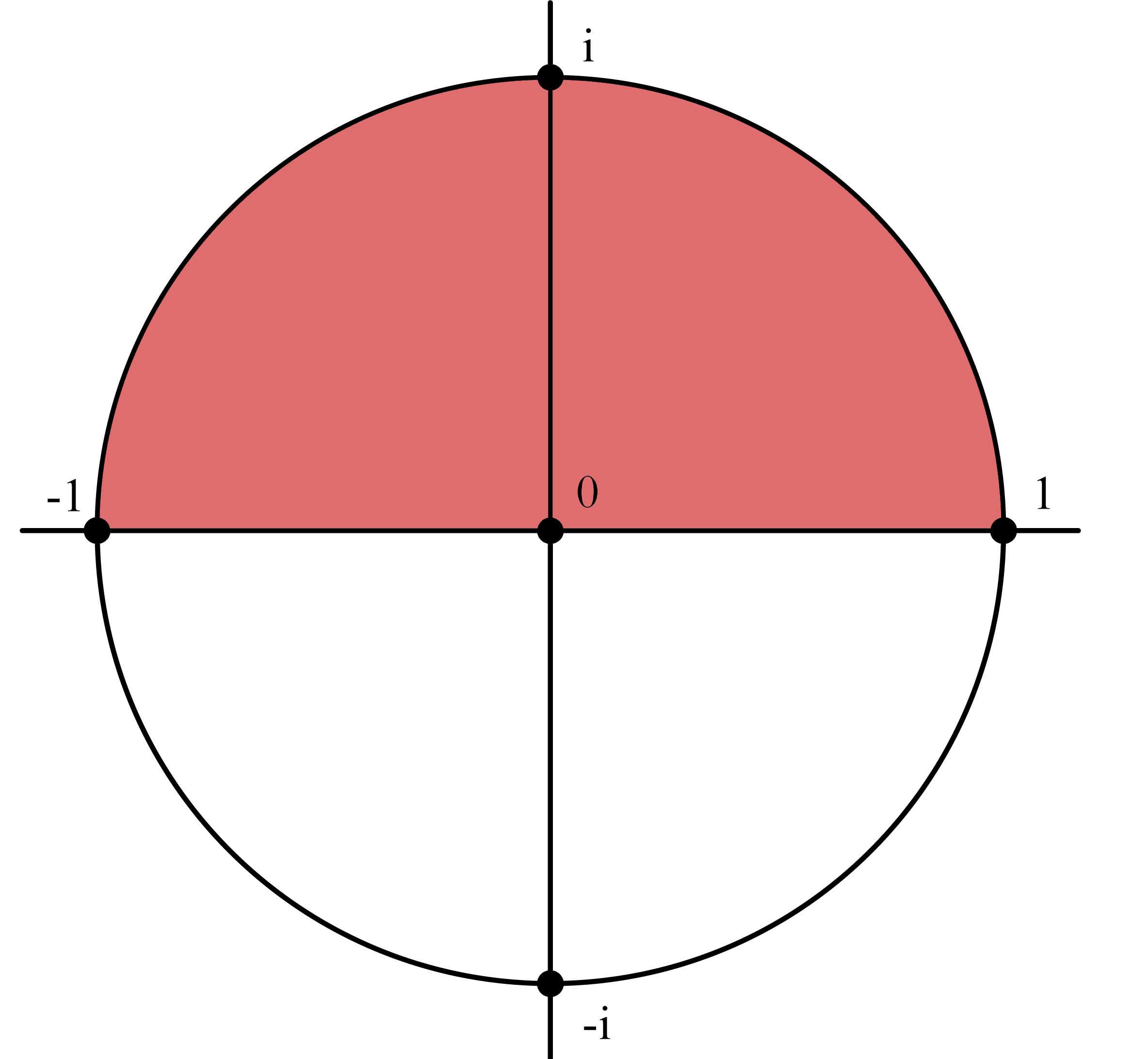
Von Gauß stammt auch die bekannte Darstellung der komplexen Zahlen als Punkte der Ebene, siehe Bild.

Beim Multiplizieren von komplexen Zahlen addieren sich die Winkel zur waagerechten Achse. Deshalb eignen sich komplexe Zahlen hervorragend zur bequemen Beschreibung von Drehungen der Ebene.

Der Ire William Rowan Hamilton (1805 - 1865) sah es als eine seiner Lebensaufgaben an, diesen Vorteil der komplexen Zahlen auch für Drehungen im dreidimensionalen Raum zu erlangen. Dazu wollte er Vektoren in diesem Raum multiplizieren und somit zu Zahlen neuer Art machen.  Er hat es jahrelang vergeblich versucht. Wir wissen heute, dass es unmöglich ist. Aber er fand einen Ausweg, er benutzte den vierdimensionalen Raum und schuf die Quaternionen. Dafür setzte er einen neuen Joker ein, den er j  nannte. Das Produkt i · j  nannte er k. Es gelten (per Dekret!) die Gleichungen

i²= j² = k² = -1, ij = k, ki = j, jk = i.

Eine Quaternion ist ein Ausdruck a + bi + cj + dk  mit reellen Zahlen a, b, c, d.  Die Rechenregel xy = yx  gilt für Quaternionen nicht mehr. Hamiltons Traum ist wahr geworden: die Quaternionen ermöglichen eine ideale Beschreibung von Drehungen im drei- und vierdimensionalen Raum. Sie sind beispielsweise aus der Raketensteuerung nicht wegzudenken und haben bei der Mondlandung  entscheidend mitgeholfen.

Erfolg macht gierig, man fragt natürlich sofort, ob es noch weitergeht. Leider ist aber hier das Ende der Fahnenstange erreicht. Man kann zwar auch noch mit Oktaven (im achtdimensionalen Raum) rechnen, wie Arthur Cayley gezeigt hat, aber dazu muss man auch die Rechenregel x(yz)=(xy)z, das Assoziativgesetz, opfern, und in noch höheren Dimensionen geht nichts mehr.

In einer anderen Richtung ist aber eine Erweiterung möglich und nützlich: Man kann zu den reellen Zahlen unendlich kleine und unendlich große Zahlen hinzunehmen und bekommt die Nichtstandard reellen Zahlen. Damit wird es möglich, beispielsweise die Differentiale dx, dy  der Analysis als legale Zahlen anzusehen, und der Differentialquotient  dx/dy  wird dann ein richtiger Quotient. Allerdings wird die Mühe, die sauberes Argumentieren in der Analysis macht, damit keineswegs überflüssig, sie wird nur verlagert.

Primzahlen und Dedekinds Idealbegriff

Gilt für natürliche Zahlen a, b, c  eine Gleichung ac = b,  so nennt man a  einen Teiler von b  und b  ein Vielfaches von a. Eine natürliche Zahl p  ≠ 1 heißt eine Primzahl, wenn sie außer 1 und sich selbst keine Teiler besitzt. Für unsere Zwecke eignet sich besser eine zweite Definition von Primzahlen, die im Fall natürlicher Zahlen auf dasselbe hinausläuft. Wir nennen p  eine Primzahl, wenn sie folgende Eigenschaft hat: Falls p  ein Produkt ab  teilt, so teilt p mindestens einen der Faktoren a  und b.

Euklid hat gezeigt, dass es unendlich viele Primzahlen gibt. Der Beweis ist sehr einfach: Gäbe es nur endlich viele, so könnte man  ihr Produkt bilden, und die hierauf folgende Zahl hätte keinen Primteiler. Außerdem zeigt Euklid, dass jede natürliche Zahl sich auf genau eine Weise als Produkt von Primzahlen darstellen lässt.

Die Begriffe Teiler, Vielfaches und Primzahl (im Sinn der zweiten Definition)  übertragen sich sinngemäß auf andere Zahlsysteme, zum Beispiel solche, die aus ganzen algebraischen Zahlen bestehen. Statt den letzteren Begriff zu definieren, greifen wir einfach eines von vielen möglichen Beispielen solcher Zahlsysteme heraus und betrachten die Menge A aller Zahlen der Form  a + bi = √5, wobei a, b gewöhnliche ganze Zahlen sind und i = √-1 die imaginäre Einheit ist. In diesem Zahlsystem gilt Euklids Satz von der Eindeutigkeit der Primfaktorzerlegung nicht. Die Zahl 9 lässt sich zum Beispiel auf zwei Weisen in Primfaktoren zerlegen, es gilt nämlich 3 · 3 = (2+ i√5) · (2- i√5).

Dieser Sachverhalt ist so unerwartet, dass der bedeutende Mathematiker Kummer einem Fehlschluss erlag, als er versucht hat, den großen Satz von Fermat zu beweisen, indem er den Satz von Euklid auf ganze algebraische Zahlen anwandte.

Der erwähnte Satz von Fermat besagt, dass es keine Gleichung der Form x^{n +} yⁿ = zⁿ

mit natürlichen Zahlen x, y, z  und einem Exponenten n  größer als 2 geben kann. Pierre de Fermat (1607 - 1665) hatte behauptet, er könne das beweisen. Inzwischen hat Andrew Wiles 1998 einen gültigen Beweis geliefert, eine mathematische Glanzleistung.

Dedekind hat nun das Dilemma der Primfaktorzerlegung von ganzen algebraischen Zahlen auf die typische plantonische Weis aufgelöst, in dem er die algebraischen Zahlen selbst hinter sich ließ und auf eine  höhere Ebene stieg, auf der der Satz von Euklid wieder gilt. Auch hierdurch ist er wie schon durch die Dedekindschen Schnitte unsterblich geworden. Wir wollen diesen Weg andeutungsweise nachzeichnen.

Sämtliche Vielfachen einer ganzen Zahl a  bilden ein Ideal  I = I (a), so nennt es Dedekind in unüberhörbarer Anlehnung an Platon, und das bedeutet:  wenn u  und v  zu I  gehören (also Vielfache von a sind), so gilt dies auch für jede Summe von Vielfachen der Zahlen u  und v. Der Begriff Ideal lässt sich wörtlich für Systeme ganzer algebraischer Zahlen anwenden, also etwa unser oben angegebenes Zahlsystem A. Unter einem Vielfachen von u  ist dann wohlgemerkt ein Produkt der Form uw  mit einer beliebigen Zahl w  aus A  zu verstehen. Anders als bei gewöhnlichen ganzen Zahlen gibt es in A allerdings viel mehr Ideale als nur die Ideale I (a), die man natürlich auch hier bilden kann.

Es ist nun zu bemerken, dass man (bei gewöhnlichen wie bei algebraischen ganzen Zahlen) das Ideal I (ab) eines Produkts leicht aus den Idealen I(a) und I(b) gewinnen kann, es ist nämlich einfach das Produkt dieser beiden Ideale, und das heißt, es besteht aus den Produkten einer Zahl aus I(a) mit einer Zahl aus I(b) und allen Summen von derartigen Produkten. Das Produktideal ist nicht etwa eine Obermenge der beiden Ideale, sondern es ist umgekehrt in beiden enthalten.

Auch die Teilerbeziehung spiegelt sich auf der Ebene der Ideale wider: a  teilt b  genau dann, wenn jedes Vielfache von b  auch Vielfaches von a  ist, also wenn I(a) eine Obermenge von I(b) ist. Gefühlt findet hier eine Richtungsumkehr statt!

Der ersten Definition von Primzahlen entsprechen daher auf der Ebene der Ideale die sogenannten maximalen Ideale, also solche, für die keine echte Obermenge wieder ein Ideal ist. Dieser Begriff hilft uns hier nicht, aber die zweite Definition der Primzahlen führt zum Begriff des Primideals. Ein Primideal P  hat also folgende Eigenschaft: Wenn P  ein Produkt IJ  von Idealen teilt (das heißt, umfasst), so teilt P  einen der Faktoren I, J.

Dedekind beweist nun den Satz von Euklid in der Idealversion: Jedes Ideal in einem System ganzer algebraischer Zahlen lässt sich auf genau eine Weise als Produkt von Primidealen darstellen.

Riemannsche Flächen

Eine sehr fruchtbare Idee von Bernhard Riemann, 1826 - 1866, soll am Beispiel des Quadrierens und Wurzelziehens bei komplexen Zahlen erläutert werden. Beim Quadrieren verdoppelt sich der Winkel zur waagerechten Achse der komplexen Zahlenebene. Daher wird die obere Hälfte der Kreisscheibe vom Radius 1 so aufgefächert, dass sie die Scheibe komplett bedeckt, und dasselbe geschieht mit der unteren Hälfte. 

Beim Versuch, Quadratwurzeln zu ziehen, hat man also die Qual der Wahl, ob man eine Wurzel in der oberen oder in der unteren Hälfte möchte. Besonders an den Nahtstellen ist das unangenehm, wie gestaltet man die Übergänge? Hierfür gibt die Riemannsche Fläche der Wurzelfunktion eine große Hilfe. Im folgenden Bild ist dies die obenliegende, mit einer Selbstdurchdringung gezeichnete Fläche.

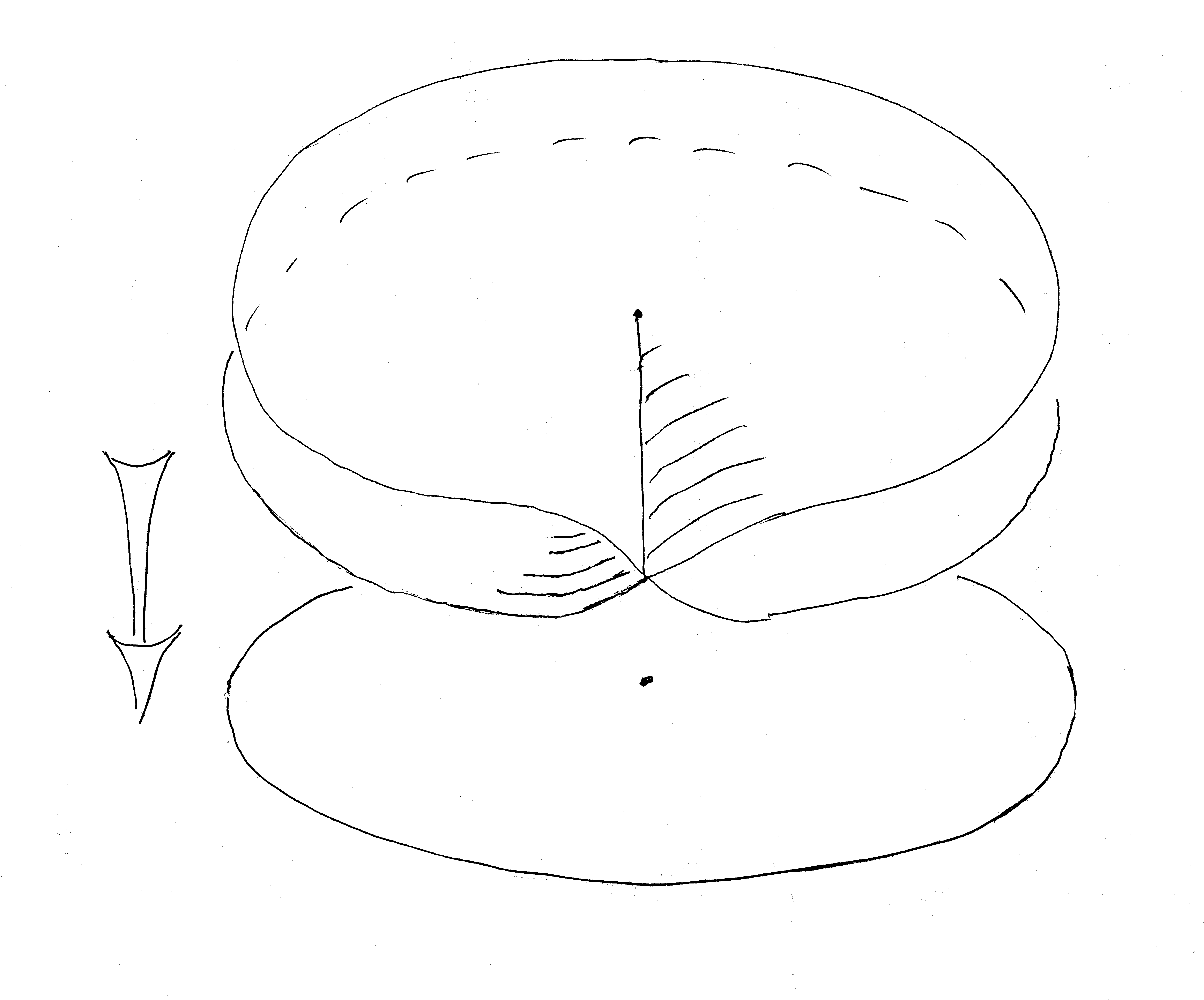
Man kann sich vorstellen, dass man beim Quadrieren zunächst in dieser oberen Etage ankommt und so noch im Gedächtnis hat, ob man von einer Stelle in der oberen oder unteren Hälfte ausgegangen ist. Erst danach wird senkrecht nach unten projiziert. Fasst man das Wurzelziehen als Abbildung von unten nach oben auf, so ist zumindest in kleinen Bereichen das Problem der Anschlüsse gut zu verstehen.

Quasikristalle

Die regelmäßige Gestalt von Kristallen kommt normalerweise daher, dass die Atome des Kristalls in einem periodischen Gitter angeordnet sind. Das heißt,  dass sich eine Anordnung weniger Atome (die beispielsweise an den Ecken eines Würfels sitzen) über den ganzen Raum hin ständig wiederholt. Man kann leicht beweisen, dass bei einer solchen Anordnung niemals die Symmetrie eines regelmäßigen Fünfecks auftreten kann. Es wurde jedoch beobachtet, dass in seltenen Ausnahmefällen Kristalle die Gestalt eines regelmäßigen Dodekaeders annehmen können, der diese Art der Symmetrie besitzt. Auch im Röntgen-Beugungsbild zeigt sich diese Symmetrie. Mathematiker haben daher nach Gitterstrukturen (Quasikristalle nennt man sie) gesucht, die dieses Phänomen erklären können. Beispiele wurden unter anderem von Roger Penrose angegeben, ein zweidimensionales ist im Bild wiedergegeben.

Es handelt sich auf den ersten Blick scheinbar auch um eine Wiederkehr eines gleichen Grundmusters über die ganze Ebene, aber bei näherer Betrachtung sieht man überall Abweichungen. Es ist schwierig, solche Strukturen zu finden. Eine Methode im Sinne des Höhlengleichnisses besteht darin, dass man ein regelmäßiges Gitter im Raum der nächstgrößeren Dimension nimmt, und den Raum R, in dem der Quasikristall entstehen soll, mit im Vergleich zum Gitter "irrationaler Steigung" in den größeren Raum hineinlegt. Nimmt man nun die Punkte des regelmäßigen Gitters in der Nähe von R, so ergeben deren Schatten in R  unter senkrecht einfallender Beleuchtung einen Quasikristall. Das folgende Bild zeigt ein Beispiel hierfür, bei dem der "Raum" R  lediglich eindimensional ist.

Wir haben nun einige ausgewählte Situationen kennengelernt, in denen mathematischer Fortschritt durch einen Schöpfungsprozess ermöglicht wird, den man im Lichte des Höhlengleichnisses deuten und interpretieren kann. Die Auswahl war bestimmt durch die Prägnanz der Beispiele und ihre Zugänglichkeit auch für Menschen ohne professionelle mathematische Vorbildung. Jeder erfahrene Mathematiker kennt bewusst oder unbewusst unzählige Beispiele dieser Art. Es handelt sich hier um einen Motor, der die Weiter- und Höherentwicklung der Mathematik seit Jahrtausenden antreibt und auch in Zukunft weiter antreiben wird.

Ein Gastbeitrag von Rainer Loewen, Braunschweig

Text sowie alle Fotos und Abbildungen von Rainer Loewen, Braunschweig. Nutzung, auch auszugsweise, nur nach Erlaubnis durch den Autor.

Der Artikel erschien erstmals als Sonderdruck der Braunschweigischen Wissenschaftlichen Gesellschaft im Jahr 2020.