Er ersann eine Rechenmaschine, entwickelte die Wahrscheinlichkeitsrechnung und veröffentlichte wegweisende Arbeiten zur Theorie des Luftdrucks, dessen Einheit heute seinen Namen trägt. Blaise Pascal, der bedeutende Mathematiker, Physiker und Philosoph wäre im Juni dieses Jahres 400 Jahre alt geworden.
Der Mathematiker, Physiker und Philosoph Blaise Pascal. Gemälde von François II Quesnel
Lizenz: CC BY 3.0
Geboren wurde der Spross einer wohlhabenden Juristenfamilie am 19. Juni 1623 im zentralfranzösischen Clermont (heute Clermont-Ferrand). Sein Vater Étienne, Richter am örtlichen Steuergerichtshof und Amateurmathematiker, erkannte schon früh die außerordentliche Begabung seines Sohnes. Um diesem die bestmögliche Förderung zu gewähren, zog die Familie 1631 nach Paris, wobei seine Mutter schon gestorben war – Blaise war zu diesem Zeitpunkt drei Jahre alt. Die frühe Förderung des jungen Pascals trug schnell Früchte und über Bekanntschaften seines Vaters in die Pariser Gelehrtenwelt kam er früh mit dekorierten Wissenschaftlern wie dem Mathematiker Père Mersenne in Kontakt. Nachdem die Familie 1640 in das Normannische Rouen gezogen war, erfand der gerade erst Neunzehnjährige Pascal eine Rechenmaschine, die als eine der ersten ihrer Art gilt und Blaupause für nachfolgende Konstruktionen werden sollte: Die Pascaline.
Eine Pascaline. Die Rechenmaschine konnte addieren und subtrahieren.
Bild: David.Monniaux, Lizenz CC BY-SA 3.0
Pascal konvertierte, wie auch seine ganze Familie, 1646 zum Jansenismus, eine radikale Spielart des Katholizismus. Der Glaube sollte später zum elementaren Bestandteil in Pascals Leben und seiner Philosophie werden. 1647, sein Vater war inzwischen verstorben, zog Pascal nach Paris, wo er, durch sein üppiges Erbe finanziell unabhängig, schnell Teil der gutbetuchten Pariser Bohème wurde: Er verkehrte unter anderem mit dem philosophisch interessierten jungen Duc de Roannez und dem Freigeist und Schriftsteller Chevalier de Méré. Zu seinen Brieffreundschaften zählte insbesondere auch der „König der Amateurmathematiker“, der Richter Pierre de Fermat. Mit Letzterem entwickelte Pascal die Grundlagen der Wahrscheinlichkeitstheorie; sie diskutierten dabei die Gewinnchancen bei Würfelspielen, denen der an Spielsucht leidende Hasardeur Méré verfallen war.
In Paris veröffentlichte er auch seine ersten Abhandlungen über Luftdruck und Hydrostatik, in denen er für das – seinerzeit kontrovers diskutierte – Konzept des Vakuums argumentierte. 1654 publizierte er die Abhandlung „Traité du triangle arithmétique“, in der er als erster Europäer Binomialkoeffizienten beschrieb, und diese in einem nach ihm benannten Dreiecksmuster, dem „Pascal’schen Dreieck“ anordnete (Tatsächlich hat Pascal das Dreieck nicht als erster entdeckt; dies gelang mehrere Jahrhunderte vorher bereits chinesischen, indischen und persischen Mathematikern).
Doch die Zeit in der Pariser Gesellschaft sollte dem jungen Pascal keine Erfüllung bringen und er änderte seinen Lebensstil radikal. 1654 zog er in ein weniger vornehmes Stadtviertel und suchte nunmehr die Gesellschaft von Theologen und Geistlichen im Umfeld des jansenistischen Klosters Port-Royal des Champs nahe Versailles. In dieser Zeit widmete er sich vermehrt theologischen Schriften – z. B. schrieb er Apologien und kommentierte die Auseinandersetzungen zwischen Jansenisten und Jesuiten. Seine mathematische Wissbegierde sollte aber nie ganz verstummten: 1659 veröffentlichte er eine Schrift „Traité des sinus des quarts de cercle“ (Abhandlung über den Sinus des Viertelkreises), die als eines der Schlüsselwerke für die Entwicklung der Differential- und Integralrechnung durch Leibniz und Newton gilt.
Zeitlebens war Pascal von vielen Krankheiten geplagt: Er litt an lahmen Beinen, Krämpfen und Schmerzen. Der Tod seiner jüngeren Schwester Jacqueline 1661 nährte seine Leiden zusätzlich und sein Zustand verschlechterte wich im folgenden Jahr dramatisch. Am 19. August 1662 starb er in Paris.
In der Mathematik wird der Name Pascals vor allem mit dem nach ihm benannten Dreieck in Verbindung gebracht, das sowohl in der Kombinatorik als auch in der Wahrscheinlichkeitstheorie von herausragender Bedeutung ist. Für die Einträge in den Zellen genügen zwei einfache Konstruktionsregeln: (a) In den Zellen außen stehen Einsen. (b) Jede weitere Zelle ist die Summe der beiden oberen Zellen. Befolgt man diese Konstruktionsregel, so ergibt sich folgendes Muster:
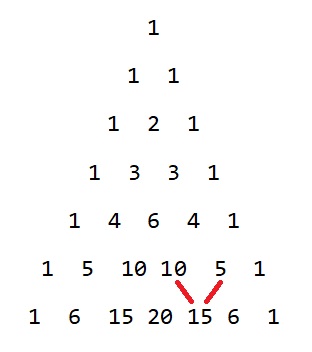Das Pascal'sche Dreieck. Der Wert in einer Zelle ist die Summe der beiden oberen Einträgen.
Bild: Konrad Krug
Die Zahlen, die in den einzelnen Zellen stehen heißen „Binomialkoeffizienten“ \({n}\choose{k}\), lies „n über k“, dabei steht \(n\) für die Zeile und \(k\) die Stelle in der jeweiligen Zeile (ab 0 gezählt); zum Beispiel ist \({{6}\choose{4}}=15\). Binomialkoeffizienten spielen für die Kombinatorik, also dem „systematischen Zählen“ eine wichtige Rolle, denn sie geben die Anzahl der Möglichkeiten an, aus \(n\) Objekten genau \(k\) Objekte auszuwählen; oder formaler: \({n}\choose{k}\) beschreibt die Anzahl der \(k\)-elementigen Teilmengen einer \(n\)-elementigen Menge. Aber wie hängen die kombinatorische Definition der Binomialkoeffizienten und die Konstruktionsregeln des Pascal‘schen Dreiecks zusammen? Betrachten wir zum Beispiel die \({{6}\choose{4}}=15\) vierelementigen Teilmengen der \(6\)-elemntigen Menge \(\{a,b,c,d,e,f\}\), nämlich \(\{a,b,c,d\}\), \(\{a,b,c,e\}\), \(\{a,b,c,f\}\), \(\{a,b,d,e\}\), \(\{a,b,d,f\}\), \(\{a,b,e,f\}\), \(\{a,c,d,e\}\), \(\{a,c,d,f\}\), \(\{a,c,e,f\}\), \(\{a,d,e,f\}\), \(\{b,c,d,e\}\), \(\{b,c,d,f\}\), \(\{b,c,e,f\}\), \(\{b,d,e,f\}\), und \(\{c,d,e,f\}\). Diese Menge teilen wir in zwei Teile auf, nämlich in solche Mengen, die das Element \(a\) enthalten und solche Mengen, die das Element \(a\) nicht enthalten. Zur Menge von Typ I gehören also die Mengen \(\{a,b,c,d\}\), \(\{a,b,c,e\}\), \(\{a,b,c,f\}\), \(\{a,b,d,e\}\), \(\{a,b,d,f\}\), \(\{a,b,e,f\}\), \(\{a,c,d,e\}\), \(\{a,c,d,f\}\), \(\{a,c,e,f\}\), \(\{a,d,e,f\}\), während zur Menge von Typ II die Mengen \(\{b,c,d,e\}\), \(\{b,c,d,f\}\), \(\{b,c,d,e\}\), \(\{b,c,d,f\}\) und \(\{c,d,e,f\}\) gehören. Die Mengen vom Typ I stehen nun in einer Eins-zu-Eins-Beziehung zu den \(3\)-elementigen Teilmengen der \(5\)-elementigen Menge \(\{b,c,d,e,f\}\), wenn man das \(a\) aus der Menge entfernt: Aus \(\{a,b,d,f\}\) etwa wird \(\{b,d,f\}\) und aus \(\{a,b,c,d\}\) wird \(\{a,b,c,d\}\). Mengen vom Typ II wiederum entsprechen genau den \(4\)-elemtigen Teilmengen der \(5\)-elementigen Menge \(\{b,c,d,e,f\}\). So ergibt sich die Formel \begin{align*}{{n}\choose{k}}={\binom{n-1}{k-1}}+{\binom{n-1}{k}}, \\ \end{align*}
die der Konstruktionsregel (b) des Pascal’schen Dreiecks entspricht: Eine Zelle ist genau die Summe der beiden oberen Zellen.
Konrad Krug